비전공자를 위해 상세한 정보들은 제외했습니다.
질문은 댓글 달아주시면 최대한 자세하게 답변드리도록 하겠습니다 :)
RSA는 정수론과 관련있는 공개키 암호 알고리즘입니다.
1977년 Ron Rivest, Adi Shamir, Leonard Adleman 3명이 인수분해의 어려움을 기반으로 한 공개키암호를 제안했습니다.
RSA는 "Rivest-Shamir-Adleman"의 약자로, RSA 암호 시스템은 공개키와 개인키라는 두 개의 키를 사용하여 데이터를 암호화하고 해독하는데 사용됩니다.
공개키는 누구나 알 수 있지만, 해당 키를 사용하여 암호화된 메시지를 해독할 수 없습니다. 개인키는 오직 키의 소유자만이 알고 있어야 하며, 이 키를 사용하여 암호화된 메시지를 해독할 수 있습니다.

여기서 공개키는 누구나 알 수 있고, 데이터를 암호화하는 데 사용됩니다. 반면에 비밀키는 오직 키의 소유자만이 알고 있으며, 암호화된 데이터를 복호화하는 데 사용됩니다.
RSA 암호화 과정 (정수론)
- 키 생성:
- 먼저, 두 소수를 선택합니다. 이 소수는 매우 크고 무작위로 선택됩니다. 이 두 소수를
p와q라고 합니다. 그런데 실제 현업에서 사용하는 소수는 사실 임의의 매우 큰 숫자를 생성한 후 소수 판변법을 사용하여 이를 통과 하면 소수 일거라고 가정하고 사용하는 가짜 소수입니다. 대표적으로 밀러-라빈 소수 판별법이 있습니다. p와q를 곱한 값을n으로 정의합니다. (n = p * q)n을 이용하여 오일러 파이 함수(φ)를 계산합니다.φ(n) = (p-1)(q-1)입니다.φ(n)과 서로소인 하나의 양수e를 선택합니다. (1 < e < φ(n))
n과e는 공개키의 일부가 되며,n은 모듈로,e는 공개 지수로 사용됩니다. - 먼저, 두 소수를 선택합니다. 이 소수는 매우 크고 무작위로 선택됩니다. 이 두 소수를
- 비밀키 생성:
e의 모듈로φ(n)에 대한 역원을 찾습니다. 즉,d * e ≡ 1 (mod φ(n))을 만족하는d를 찾습니다. 이d는 비밀키의 일부가 됩니다. 역원 계산은 확장 유클리드 알고리즘을 이용합니다.
- 공개키 및 비밀키의 배포:
n과e는 공개키로,n과d는 비밀키로 사용됩니다.n은 모둘로 사용되며,e는 공개 지수입니다.d는 비밀 키로 사용됩니다.
- 암호화:
- 메시지나 데이터를 암호화하기 위해 공개키
(n, e)를 사용합니다. - 메시지를 숫자로 변환한 후,
c = m^e mod n을 계산하여 암호문을 생성합니다.
- 메시지나 데이터를 암호화하기 위해 공개키
- 복호화:
- 암호문
c를 복호화하기 위해 비밀키d를 사용합니다. m = c^d mod n을 계산하여 원래의 메시지를 복원합니다.
- 암호문
RSA는 n을 소인수분해하는 것이 어려워서 보안적으로 강력한 암호화 방법으로 알려져 있습니다. 또는 d 값을 알아내야 비밀정보를 얻을 수 있는데 이것이 어렵다는 것을 이산로그문제 또는 이산 대수 문제 라고 합니다. 또한 현업에서는 RSA-CRT, RSA-OAEP 등 조금 더 복잡한 방법을 사용합니다.
RSA 실생활 적용 예제
가장 쉽게 주위에서 볼 수 있는 방법을 알려드리겠습니다. 현재 저는 chrome 웹 브라우저를 사용하고 있어서 이를 기준으로 설명드리겠습니다. 해당 예시는 모든 웹 브라우저 인증서에서 확인 가능합니다.
인증서란?
인증서는 공개키 기반의 암호화 시스템에서 사용되는 중요한 보안 도구입니다. 인증서는 디지털 문서로서, 특히 웹사이트나 온라인 서비스와 같은 네트워크 통신에서 사용됩니다.
인증서에는 다음과 같은 정보가 포함될 수 있습니다.
- 공개키: 공개키는 해당 인증서와 연결된 공개키 암호화 시스템에서 사용되는 키입니다. 이 키를 사용하여 데이터를 암호화할 수 있으며, 이를 해독하는 데에는 해당 공개키에 대응하는 개인키가 필요합니다.
- 인증서 소유자 정보: 인증서에는 보통 해당 공개키의 소유자(일반적으로는 웹사이트 또는 서버의 소유자) 정보가 포함됩니다. 이 정보에는 조직명, 도메인 주소 등이 포함될 수 있습니다.
- 발급자 정보: 인증서를 발급한 인증 기관의 정보가 포함됩니다. 이 기관은 공개키를 소유자에게 제공하고 이를 검증하는 역할을 합니다.
- 유효 기간: 인증서는 발급일과 만료일을 포함하여 유효 기간을 가지고 있습니다. 만료일 이후에는 해당 인증서를 사용할 수 없습니다.
- 디지털 서명: 인증서에는 인증 기관의 개인키로 생성된 디지털 서명이 포함됩니다. 이 서명을 통해 누구나 해당 공개키를 신뢰할 수 있음을 검증할 수 있습니다.
웹 브라우저 등의 클라이언트가 웹사이트에 접속할 때, 서버는 자신의 인증서를 제공하여 클라이언트에게 보냅니다. 클라이언트는 해당 인증서를 사용하여 서버의 공개키를 확인하고, 암호화된 통신을 시작합니다. 이를 통해 데이터의 안전한 전송이 보장됩니다.
저는 naver에서 인증서를 확인해보겠습니다. 어느 웹 사이트이든 상관없습니다.
자물쇠 버튼을 클릭합니다. 이 방법 사용하는 웹 브라우저에 따라 달라질 수 있습니다. "이 연결은 안전합니다." 를 클릭합니다.
그럼 이런 화면이 뜹니다. 저희는 인증서에서 RSA 암호 알고리즘이 사용되었는지 확인해 보겠습니다. "인증서가 유효함" 을 클릭합니다.
그럼 인증서 뷰어가 뜹니다. 여기서 정리된 인증서 정보를 확인 할 수있습니다.
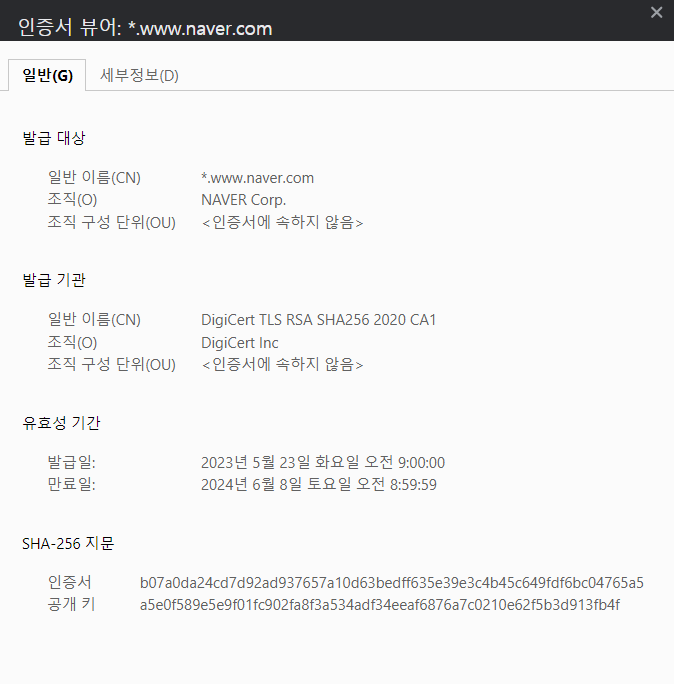
세부정보로 가보면 여러 정보들을 확인 할 수있습니다.
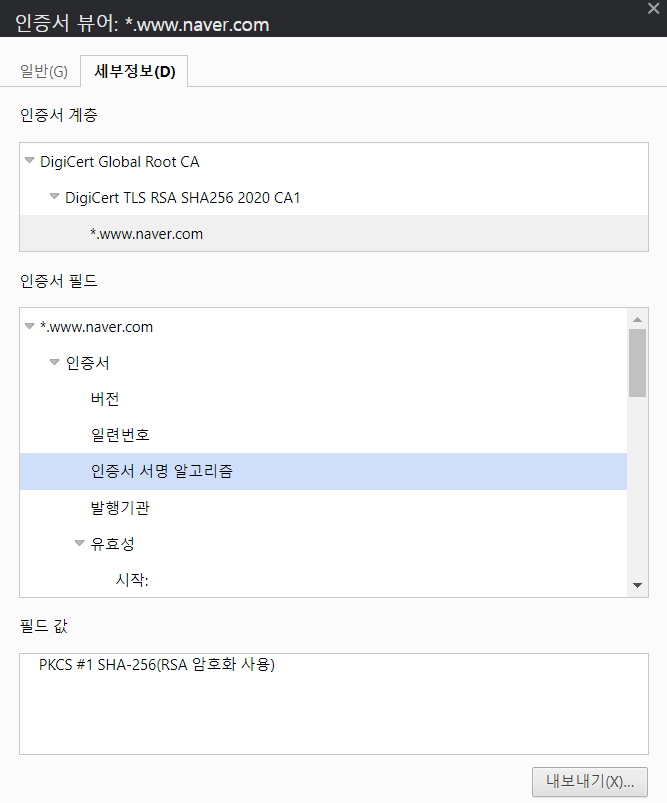
인증서 서명 알고리즘을 클릭하면 하단에 RSA 암호화 사용이라고 적혀있습니다.
OpenSSL을 이용한 RSA
이번에는 OpenSSL을 통해 RSA인증서를 생성 해보겠습니다.
리눅스가 있으면 일반적으로 OpenSSL이 설치되어 있기에 그대로 사용하면 됩니다. 만약 아니라면 Online terminal사이트를 이용하시면 됩니다.
Online Linux Terminal
Free access for unlimited time Limited trial with credit cardFull LinuxCount of of pre-installed packages, by running 'apt list --installed | wc -l' or 'rpm -qa | wc -l' ~ 9500N/A ~ 200 ~ 700Copy/pastePeriodic backups of your dataPersistent of your dataEas
cocalc.com
Online terminal 사이트에 접속하면 아래와 같은 화면이 보이실 겁니다. Edit 버튼을 눌러줍니다.
이후 openssl version 명령어를 입력하여 설치 확인 및 버전을 확인합니다. 2023년 11월 기준으로 해당 Online terminal 사이트는 OpenSSL 1.1.1f 버전을 사용하고 있습니다.
아래 명령어를 입력해주고 Run 버튼을 눌러줍니다.
$ openssl genpkey -algorithm RSA -pkeyopt rsa_keygen_bits:1024 -pkeyopt rsa_keygen_pubexp:65537 -text그 결과는 아래와 같고 RSA-CRT 형식으로 출력됩니다.
.....++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
................................................++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
-----BEGIN PRIVATE KEY-----
MIICdgIBADANBgkqhkiG9w0BAQEFAASCAmAwggJcAgEAAoGBALmmR1s4Ni8Tzgpy
pB8Zf0iHWUZnjy+0HKprM1poCEeEJFvLraTzF43OFG74lJEiOxl9vQoV9tRdKA5U
5zdFiowmZ+4AsB8N7ADGDmvCpaYtJyO4Pp52pH+Z2JB3erb+9L3UzzOS9Pt3eizT
j3wSSKc81c8Ym0cPdrun2ypDpTU/AgMBAAECgYA8VmKSry5NFq68jo3w3aSUugi1
7SqIYo1+heDm3TDzrWrzurrxBWD+YaAagQgoM2vp2Qf7oy/ZzX0bS1Tqjdt9K2i3
c1DHVTUEzN4c3jC20hHKX2wqBOf+NckjZaieoSFuqbr061YA7rCXLKl/h8V7+MGV
EJ6TNdFl7YwzY6gSoQJBAOj9Pi0zO4F+QcRlJB0NMvHGvbnhj7/aTsC896iQ5KGj
9AxWYMY09vGM5AYD1Io5Kbg0ZtOWeFpPdYu3LUvjZ7MCQQDL/CC0w90tw7p2+kP9
UEb4KQK0M4DU3FNkiJGo1nGqFz6p7L+vucPB9FQ6z+s0u/BXtaxRSEJGhnc1EOQd
W7ZFAkEA2s0IWRZl6aQSS0fYdFfy4c+MWUYU40027BYKVolLzOjVxchQtZMD3bA8
a9GpBe3M2iqL7mS+vcElWII7zarPtQJAQrd9DwJ8xeodg6qJMEHgZGwtaTjrKzPA
xsHwOjOhS4t8wGEhtNziTP6XygCVIlNR4a4W5SLoIl76gE28/mkvrQJAF97E/kvS
1ezm6E6u4O3iRhHM3jHl4eyV+EYrt+nmkbVBZCqTBEnmp9uI2VTjACsumPpSL/d/
VuCqWNi0K9FTqA==
-----END PRIVATE KEY-----
Private-Key: (1024 bit, 2 primes)
modulus:
00:b9:a6:47:5b:38:36:2f:13:ce:0a:72:a4:1f:19:
7f:48:87:59:46:67:8f:2f:b4:1c:aa:6b:33:5a:68:
08:47:84:24:5b:cb:ad:a4:f3:17:8d:ce:14:6e:f8:
94:91:22:3b:19:7d:bd:0a:15:f6:d4:5d:28:0e:54:
e7:37:45:8a:8c:26:67:ee:00:b0:1f:0d:ec:00:c6:
0e:6b:c2:a5:a6:2d:27:23:b8:3e:9e:76:a4:7f:99:
d8:90:77:7a:b6:fe:f4:bd:d4:cf:33:92:f4:fb:77:
7a:2c:d3:8f:7c:12:48:a7:3c:d5:cf:18:9b:47:0f:
76:bb:a7:db:2a:43:a5:35:3f
publicExponent: 65537 (0x10001)
privateExponent:
3c:56:62:92:af:2e:4d:16:ae:bc:8e:8d:f0:dd:a4:
94:ba:08:b5:ed:2a:88:62:8d:7e:85:e0:e6:dd:30:
f3:ad:6a:f3:ba:ba:f1:05:60:fe:61:a0:1a:81:08:
28:33:6b:e9:d9:07:fb:a3:2f:d9:cd:7d:1b:4b:54:
ea:8d:db:7d:2b:68:b7:73:50:c7:55:35:04:cc:de:
1c:de:30:b6:d2:11:ca:5f:6c:2a:04:e7:fe:35:c9:
23:65:a8:9e:a1:21:6e:a9:ba:f4:eb:56:00:ee:b0:
97:2c:a9:7f:87:c5:7b:f8:c1:95:10:9e:93:35:d1:
65:ed:8c:33:63:a8:12:a1
prime1:
00:e8:fd:3e:2d:33:3b:81:7e:41:c4:65:24:1d:0d:
32:f1:c6:bd:b9:e1:8f:bf:da:4e:c0:bc:f7:a8:90:
e4:a1:a3:f4:0c:56:60:c6:34:f6:f1:8c:e4:06:03:
d4:8a:39:29:b8:34:66:d3:96:78:5a:4f:75:8b:b7:
2d:4b:e3:67:b3
prime2:
00:cb:fc:20:b4:c3:dd:2d:c3:ba:76:fa:43:fd:50:
46:f8:29:02:b4:33:80:d4:dc:53:64:88:91:a8:d6:
71:aa:17:3e:a9:ec:bf:af:b9:c3:c1:f4:54:3a:cf:
eb:34:bb:f0:57:b5:ac:51:48:42:46:86:77:35:10:
e4:1d:5b:b6:45
exponent1:
00:da:cd:08:59:16:65:e9:a4:12:4b:47:d8:74:57:
f2:e1:cf:8c:59:46:14:e3:4d:36:ec:16:0a:56:89:
4b:cc:e8:d5:c5:c8:50:b5:93:03:dd:b0:3c:6b:d1:
a9:05:ed:cc:da:2a:8b:ee:64:be:bd:c1:25:58:82:
3b:cd:aa:cf:b5
exponent2:
42:b7:7d:0f:02:7c:c5:ea:1d:83:aa:89:30:41:e0:
64:6c:2d:69:38:eb:2b:33:c0:c6:c1:f0:3a:33:a1:
4b:8b:7c:c0:61:21:b4:dc:e2:4c:fe:97:ca:00:95:
22:53:51:e1:ae:16:e5:22:e8:22:5e:fa:80:4d:bc:
fe:69:2f:ad
coefficient:
17:de:c4:fe:4b:d2:d5:ec:e6:e8:4e:ae:e0:ed:e2:
46:11:cc:de:31:e5:e1:ec:95:f8:46:2b:b7:e9:e6:
91:b5:41:64:2a:93:04:49:e6:a7:db:88:d9:54:e3:
00:2b:2e:98:fa:52:2f:f7:7f:56:e0:aa:58:d8:b4:
2b:d1:53:a8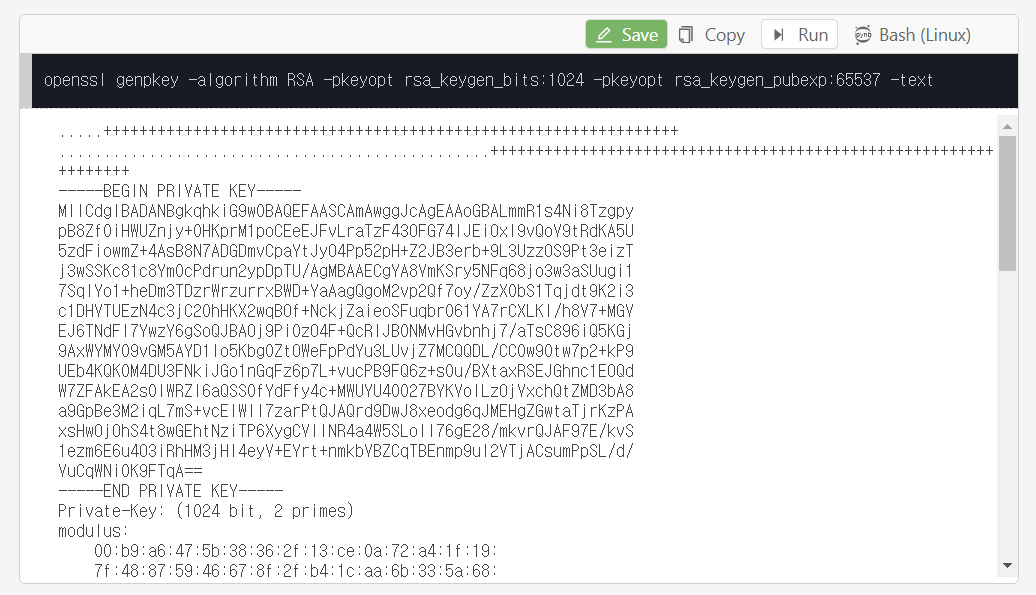
이외에 명령어 옵션은 공식사이트에서 확인 가능합니다.
https://www.openssl.org/docs/man1.0.2/man1/openssl-genpkey.html
/docs/man1.0.2/man1/openssl-genpkey.html
genpkey NAME openssl-genpkey, genpkey - generate a private key SYNOPSIS openssl genpkey [-out filename] [-outform PEM|DER] [-pass arg] [-cipher] [-engine id] [-paramfile file] [-algorithm alg] [-pkeyopt opt:value] [-genparam] [-text] DESCRIPTION The genpke
www.openssl.org
RSA sage code (Python)
SageMath 이라는 Python 라이브러리를 활용했다고 생각해주시면 될 것 같습니다. 따라서 Python 문법을 따릅니다.
테스트는 아래 사이트에서 하실 수 있습니다.
https://sagecell.sagemath.org/
Sage Cell Server
Type some Sage code below and press Evaluate. About SageMathCell About SageMathCell project is an easy-to-use web interface to a free open-source mathematics software system SageMath. You can help SageMath by becoming a . It allows embedding Sage computati
sagecell.sagemath.org
RSA 테스트 코드
# 큰 두 소수 p, q 입력
p = 7933311117131
q = 3313371113473
# 평문 입력
m = "암호학"
m1= int.from_bytes(m.encode('utf-8'), "big")
print("암호화 전 평문:", m1)
# p, q가 소수라면 RSA 암호화 테스트 실행
if is_prime(p) and is_prime(q):
# 공개키
e = 65537
n = p*q
#오일러 파이함수
phi = (p-1)*(q-1)
#개인키 생성 with 확장 유클리드 알고리즘
d = (e.xgcd(phi)[1])%phi
#암호화
s = pow(m1,e,n)
print("암호문:", s)
#복호화
mprime = pow(s,d,n)
j = bytes.fromhex(hex(mprime)[2:]).decode('utf-8')
print("복호문(숫자) =",mprime)
print("복호문(문자) =",j)
else:
print("p 가 소수인가? - ", is_prime(p))
print("q 가 소수인가? - ", is_prime(q))'암호학 강의' 카테고리의 다른 글
| ChaCha20 stream cipher (1) | 2024.02.09 |
|---|---|
| [암호학] 해시함수 Hash Function (0) | 2023.11.09 |
| [암호학] 운용모드(운영모드) Modes of Operation (0) | 2023.11.05 |
| [암호학] 국산 블록 암호 LEA (1) | 2023.11.02 |
| [암호학] AES 블록암호 코드 with 설명 (1) | 2023.10.31 |