[암호학] AES 블록암호 코드 with 설명
AES(Advanced Encryption Standard)는 현재 전 세계적으로 사용되는 대칭키 암호화 알고리즘 중 하나입니다. AES는 미국 국가표준기술연구소(NIST)에서 2001년에 공식적으로 표준으로 채택되었으며, DES(데이터 암호화 표준)의 후속 제품으로 개발되었습니다.
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf
AES가 개발된 배경
- DES의 한계: DES는 1970년대에 개발되었으며, 그 당시에는 충분히 안전한 수준으로 여겨졌습니다. 그러나 시간이 지남에 따라 컴퓨팅 파워가 증가하면서 DES의 키 공간이 너무 작아져서 더 이상 안전하지 않게 되었습니다.
- 암호학적 요구사항의 변화: 더 안전한 암호화 알고리즘이 필요해졌으며, 미국 정부는 이에 대응하여 AES의 개발을 주도하게 되었습니다.
AES 개발 과정
- 선정 과정: AES는 1997년부터 2000년까지 약 3년간에 걸쳐서 NIST가 주도하는 열린 경쟁(Open Competition)을 통해 선정되었습니다. 이 기간 동안에 다양한 후보 알고리즘이 제안되고 평가되었습니다.
- 후보 알고리즘들: 총 15개의 후보 알고리즘이 경쟁에 참가했으며, 이 중에서 5개가 최종 후보로 남았습니다. 이들은 MARS, RC6, Rijndael, Serpent, Twofish입니다.
- Rijndael의 선택: 최종적으로 Rijndael이 AES로 선정되었습니다. Rijndael은 벨기에의 두 암호학자, Vincent Rijmen과 Joan Daemen이 개발한 알고리즘으로, 뛰어난 보안성과 효율성을 갖추고 있어 선택되었습니다.
AES의 특징(매우 중요)
- 키 길이: AES는 키의 길이에 따라 세 가지 버전이 있습니다. AES-128은 128비트 마스터 키를 사용하며, AES-192와 AES-256은 각각 192비트와 256비트 마스터 키를 사용합니다. 마스터 키를 이용해 라운드 키를 생성하는데 라운드 키는 각 라운드에서 사용되는 키를 의미합니다.
- 블록 크기: AES는 128비트 블록 크기를 가지며, 평문을 128비트 블록 단위로 암호화합니다.
- 라운드: AES는 라운드(rounds)라는 순환 작업을 통해 암호화를 수행합니다. 라운드의 수는 키의 길이에 따라 달라지며, AES-128은 10라운드, AES-192는 12라운드, AES-256은 14라운드를 수행합니다.
- SubBytes, ShiftRows, MixColumns, AddRoundKey: AES 알고리즘은 이러한 네 개의 기본 연산을 사용하여 데이터를 암호화합니다.
사실 AES 구현시 유한체(갈루아 필드)라는 대수학에서 나오는 개념을 아는게 좋습니다만 이 개념을 몰라도 코딩을 하는데 문제는 없습니다. 따라서 수학적인 내용은 언급은 하지만 그렇구나 하고 넘어가는 정도로 하겠습니다. 기본적으로 비트와 바이트 정도의 개념은 아는 것으로 가정하겠습니다.
AES SW구현에 들어가며
AES의 전체적인 구조는 다음 그림과 같습니다. 여기서 N은 라운드 수이며 AES-128 기준으로 N 은 10입니다. 그리고 암호화 마지막 라운드에는 MixColumns이 빠져있는데 이 과정이 없어짐으로써 고속구현이나 복호화 시 구현의 편리함이 좋아집니다.

혹시 복호화 과정과 암호화 과정이 뭔가 비슷하다고 느껴지지 않으셨나요? 일반적으로 암호문을 가지고 암호화 과정을 반대로 거슬러 올라가면 평문을 얻을 수 있었습니다. 그런데 AES는 암호화 과정을 거슬러 올라가지 않습니다. 뭔가 이상합니다.
간단하게 말하자면 같은 라운드에 속한 ShiftRows와 SubBytes 연산끼리, AddRoundKey와 InvMixColumns 연산끼리는 서로 순서를 바꿀 수 있습니다. 이는 각 연산이 어떻게 이루어지는지 알아야 이해가 가능한 부분이라 지금 다루지 않겠습니다. 질문이 있다면 댓글 부탁드립니다.
AES는 128비트 즉, 16바이트 단위로 암복호화를 진행합니다.
C언어로 설명은 하되 파이썬 코드는 요즘 chatGPT 같은 게 워낙 잘 나와있어서 굳이 올리진 않겠습니다.
AES 구조 정의
AES는 함수라고 생각하시면 됩니다. 함수를 중학교 때 처음 배우 실 텐데 어렵게 생각할 필요 없습니다. 함수란 수를 넣는 상자입니다. 이 상자에 어떤 수를 넣어주면 정해진 규칙에 따라 결과 값을 돌려주는 것입니다.
아래와 같은 그림을 많이 보셨을텐데 정말 이게 다입니다. 수학적으로 정의하려다 보니 어렵게 생각하신 분들이 많으셨을 거라 생각합니다.

그럼 함수 AES에 들어가는 \(input\)이라는16 바이트(128 비트) 평문을 아래 그림처럼 정의할 겁니다. \(output\)은 16 바이트 암호문입니다.
AES의 \(input = a_0 || a_1 || a_2 || ... || a_{15}\) 단, \(a_i\) 들 1 바이트를 의미합니다. 반드시 이 행렬 형태로 모든 연산이 진행되니 꼭 기억해 주세요.
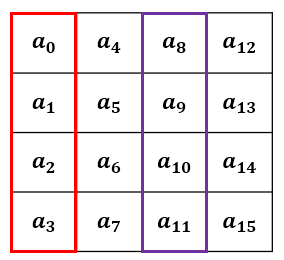
코드로는 이렇게 나타내겠습니다.
unsigned char input[16] = { 0x32, 0x43, 0xf6, 0xa8, 0x88, 0x5a, 0x30, 0x8d, 0x31, 0x31, 0x98, 0xa2, 0xe0, 0x37, 0x07, 0x34 };
AES의 한 라운드는 다음과 같이 생겼습니다. 이런 구조를 최소 10번 통과해 암호문이 만들어지게 되는 겁니다.

각 단계는 아직 설명 안 했으니 잘 모르는 게 정상입니다. 대신 가장 위에 Byte Sub(SubBytes)라는 부분에 16개의 박스들이 보이시나요? 저희가 방금 \(input\)이라는 16바이트를 1바이트씩 정의했었죠. 즉, 저 박스들이 1바이트를 의미합니다.
그럼 이제 저 단계들이 뭔지 설명하겠습니다.
1. SubBytes ( Byte Sub )
S-Box라는 게 존재합니다. 이 S-Box도 사실은 유한체(갈루아 필드)를 기반으로 만들어진 함수입니다. 행렬의 아핀 변환의 개념도 나오는데 이런 것들 몰라도 S-Box는 사전에 계산된 걸 사용하는 게 대부분이기 때문에 그냥 값만 대입하면 됩니다.
참고로 비선형함수입니다. 이는 부채널 공격(side channel attack)이라는 아주 강력한 공격을 가능하게 해주는 성질이기도 하니 이 정도는 알고 가시는 걸 추천합니다.

S-Box는 코드로 구현하면 아래 코드와 같이 나타낼 수 있습니다.
const unsigned char SBox[256] = {
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 };그럼 애를 어떻게 쓰느냐! 사실 위 그림이랑 같습니다. 각 1바이트 블록 값들을 S-Box에 대입하고 나온 결괏값을 다시 그대로 같은 위치에 넣어줍니다. 코드로는 아래와 같이 함수를 만들 수 있습니다.
void SubBytes(unsigned char state[16])
{
for (int i = 0; i < 16; i++)
state[i] = SBox[state[i]];
}
2. ShiftRows
바이트들을 이동시켜주는 단계입니다.

- 2행은 왼쪽으로 1칸 이동
- 3행은 왼쪽으로 2칸 이동
- 4행은 왼쪽으로 3칸 이동
이 그림이 ShiftRows 연산을 하기 전 초기 상태라고 합시다.

ShiftRows 연산을 거치고 나온 결과는 다음과 같습니다.
| \(a_{0}\) | \(a_{4}\) | \(a_{8}\) | \(a_{12}\) |
| \(a_{5}\) | \(a_{9}\) | \(a_{13}\) | \(a_{1}\) |
| \(a_{10}\) | \(a_{14}\) | \(a_{2}\) | \(a_{6}\) |
| \(a_{15}\) | \(a_{3}\) | \(a_{7}\) | \(a_{11}\) |
단순하게 행 단위로 바이트 블록들의 위치가 회전하는 방식입니다.
바로 이해가 되신 분들도 계시겠지만 아닐 수도 있으니 바로 코드를 보겠습니다.
void ShiftRows(unsigned char state[16])
{
// 값을 임시 저장할 변수들
unsigned char x, y, z;
// 2번째 행 1칸 이동(회전)
x = state[1];
state[1] = state[5];
state[5] = state[9];
state[9] = state[13];
state[13] = x;
// 3번째 행 2칸 이동(회전)
x = state[2], y = state[6];
state[2] = state[10];
state[6] = state[14];
state[10] = x;
state[14] = y;
// 4번째 행 2칸 이동(회전)
x = state[3], y = state[7], z = state[11];
state[3] = state[15];
state[7] = x;
state[11] = y;
state[15] = z;
}3. MixColumns
이 부분이 사실 제일 어렵습니다. 기본적으로 유한체 이론을 피해 갈 수도 없는 부분이라 최대한 간단하게 설명하겠습니다.
계수가 0 또는 1인 모든 3차 이하 다항식은 컴퓨터에서는 다음과 같이 표현할 수 있습니다.
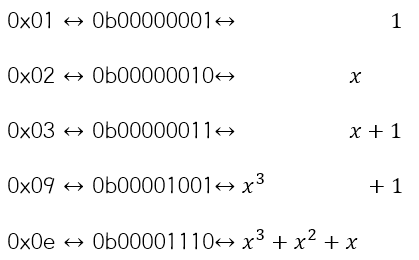
갈루아 필드에 대해 짧게 설명하자면 우리가 일반적으로 생각하는 정수 집합에서 \( 0 + 0 = 0, 1 + 0 = 1, 1 + 1 = 2 \) 이 결과는 당연합니다. 그런데 갈루아 필드 \(GF(2)\) 라는 세계에서는 조금 다릅니다. \( 0 + 0 = 0, 1 + 0 = 1, 1 + 1 = 0 \) 라는 결과가 나타납니다. 그냥 일반 덧셈이 아니라 더한 두 숫자의 결과에 2로 나눈 나머지가 덧셈의 결과물이 되는 것이죠. 수식으로는 \(1 + 1\) \(mod\) \(2\) \(= 0 \) 이렇게 나타낼 수 있습니다.
그런데 이 MixColumns이라는 녀석은 덧셈도 아니고 심지어 행렬 곱셈을 사용합니다. 말이 행렬 곱셈이지 저희가 아는 일반적인 것과 다릅니다. 각 행렬 성분끼리의 갈루아 필드 곱셈 후 일반적인 덧셈대신 갈루아 필드 덧셈( 컴퓨터에서는 Xor연산)을 사용합니다.
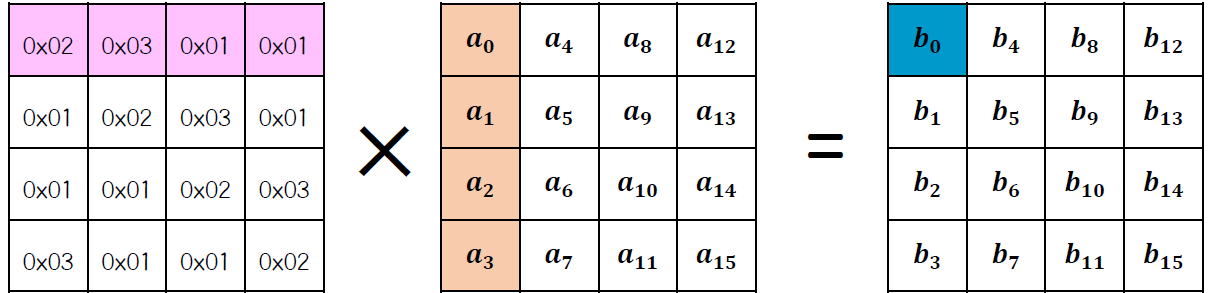
\(b_0 = 2*a_0\) ⊕ \(3*a_1\) ⊕ \(a_2\) ⊕ \(a_3\) 이렇게 표현됩니다.
사실 알고나면 진짜 별거 아닌데 수학부터 시작하는 건 좀 힘들 것 같습니다.
그냥 결과만 예시로 들어 정리하자면 다음과 같습니다.
\(a_2, a_3\) 은 1을 곱하는 연산이라 저희가 아는 대로 \(a_2, a_3\) 그대로 곱셈 결과가 나옵니다. 문제는 \(0x02, 0x03\) 연산을 수행할 \(a_0, a_1\) 입니다. 1 바이트인 \(a_0\)를 2진법(비트)으로 표현하면 다음과 같습니다.
\( a_0 = (c_7, c_6, ... , c_1, c_0)_2\)
그리고 2의 곱셈은 \(c_7\) 값에 따라 2가지 경우가 있습니다.
\(2*a_0 = a_0\) ≪ \(1\) ⊕ \(0b00011011\) \(if c_7 = 1 \)
\(2*a_0 = a_0\) ≪ \(1\) \(if c_𝟕 = 0 \)
이것만 안다면 3의 곱셈은 쉽습니다. \(a_1\)를 2진법(비트)으로 다음과 같이 나타내겠습니다.
\( a_1 = (c_7, c_6, ... , c_1, c_0)_2\)
그럼 3 곱셈은 2의 곱셈 방법을 재활용하는 방식으로 사용가능합니다.
\(3*a_1 = (2 + 1)*a_1 = 2*a_1\) ⊕ \(a_1\)
이를 코드로 옮길 건데 보기 편하게 나타내겠습니다.
// 0x02 곱셈
unsigned char mix2(unsigned char a) {
unsigned char x;
if (a >> 7 == 0) {
x = a << 1;
}
else {
x = (a << 1) ^ 0b00011011;
}
return x;
}
// 0x03 곱셈
unsigned char mix3(unsigned char a) {
unsigned char x;
if (a >> 7 == 1) {
x = (a << 1) ^ 0b00011011 ^ a;
}
else {
x = (a << 1) ^ a;
}
return x;
}이제 MixColumns 함수를 코드를 다음과 같이 노가다로 적어봤습니다. 행렬 곱셈한다고 생각하고 이해하시면 쉬울 듯합니다.
void MixColumns(unsigned char state[16])
{
unsigned char state2[16] = { 0, };
for (int k = 0; k < 16; k++)
state2[k] = state[k];
state[0] = mix2(state2[0]) ^ mix3(state2[1]) ^ state2[2] ^ state2[3];
state[4] = mix2(state2[4]) ^ mix3(state2[5]) ^ state2[6] ^ state2[7];
state[8] = mix2(state2[8]) ^ mix3(state2[9]) ^ state2[10] ^ state2[11];
state[12] = mix2(state2[12]) ^ mix3(state2[13]) ^ state2[14] ^ state2[15];
state[1] = state2[0] ^ mix2(state2[1]) ^ mix3(state2[2]) ^ state2[3];
state[5] = state2[4] ^ mix2(state2[5]) ^ mix3(state2[6]) ^ state2[7];
state[9] = state2[8] ^ mix2(state2[9]) ^ mix3(state2[10]) ^ state2[11];
state[13] = state2[12] ^ mix2(state2[13]) ^ mix3(state2[14]) ^ state2[15];
state[2] = state2[0] ^ state2[1] ^ mix2(state2[2]) ^ mix3(state2[3]);
state[6] = state2[4] ^ state2[5] ^ mix2(state2[6]) ^ mix3(state2[7]);
state[10] = state2[8] ^ state2[9] ^ mix2(state2[10]) ^ mix3(state2[11]);
state[14] = state2[12] ^ state2[13] ^ mix2(state2[14]) ^ mix3(state2[15]);
state[3] = mix3(state2[0]) ^ state2[1] ^ state2[2] ^ mix2(state2[3]);
state[7] = mix3(state2[4]) ^ state2[5] ^ state2[6] ^ mix2(state2[7]);
state[11] = mix3(state2[8]) ^ state2[9] ^ state2[10] ^ mix2(state2[11]);
state[15] = mix3(state2[12]) ^ state2[13] ^ state2[14] ^ mix2(state2[15]);
}4. AddRoundKey
이 부분은 어렵지 않습니다. 마스터 키를 이용해 라운드 키를 생성한다고 했는데 라운드 키가 여기서 사용됩니다.
마스터 키를 이용해 라운드 키를 생성하는 과정을 키 생성 함수 (Keyschedule)이라고 합니다. 사실 AES 동작 특성상 Keyschedule에 대해 설명하고 각 단계연산들에 대해 설명드려야 했지만 순서를 뒤로 넘긴 이유가 제 생각에 2번째로 어려운 부분이고 SubBytes를 먼저 다루고 가는 게 맞을 것 같았습니다.
연산은 라운드 키와 input 값들을 Xor 해주는 게 전부입니다.

코드를 보겠습니다.
void AddRoundKey(unsigned char state[16], const unsigned char roundKey[16])
{
for (int i = 0; i < 16; i++)
{
state[i] = state[i] ^ roundKey[i];
}
}정말 간단합니다.
5. 키 생성 함수 (Keyschedule)
AES-128을 기준으로 설명하겠습니다. \(k_i\) 들이 바로 마스터 키를 1바이트로 나타낸 것입니다. \(w_i\)는 4바이트 단위입니다. 즉, \(w_0 = k_0||k_1||k_2||k_3\) 으로 표현할 수 있습니다.

\(w_i\) 들이 4개씩 묶여 라운드 키가 됩니다. g함수를 보면 RC (라운드 상수)라는 게 있는데 이 친구는 사전에 주어진 값입니다. 다음과 같이 정해져 있습니다. 그리고 S 함수가 있는데 SubBytes 연산에서 사용한 S-Box입니다. 이를 알고 나면 사실 크게 특별한 연산은 없습니다.
const unsigned char roundConstant[10] = { 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36 };저 그림을 그대로 코드로 구현하면 다음과 같습니다. 엄청 긴데 사실 이해를 돕고자 다 쓴 거지 잘 보시면 같은 구조가 계속 반복됩니다.
void KeyExpansion(unsigned char roundKey[11][16], const unsigned char masterKey[16])
{
for (int j = 0; j < 16; j++) //word 0~3
roundKey[0][j] = masterKey[j];
roundKey[1][0] = roundKey[0][0] ^ roundConstant[0] ^ SBox[roundKey[0][13]];//G func
roundKey[1][1] = roundKey[0][1] ^ SBox[roundKey[0][14]];
roundKey[1][2] = roundKey[0][2] ^ SBox[roundKey[0][15]];
roundKey[1][3] = roundKey[0][3] ^ SBox[roundKey[0][12]];
for (int i = 0; i < 12; i++)//word4~7
roundKey[1][i + 4] = roundKey[1][i] ^ roundKey[0][i + 4];
roundKey[2][0] = roundKey[1][0] ^ roundConstant[1] ^ SBox[roundKey[1][13]];
roundKey[2][1] = roundKey[1][1] ^ SBox[roundKey[1][14]];
roundKey[2][2] = roundKey[1][2] ^ SBox[roundKey[1][15]];
roundKey[2][3] = roundKey[1][3] ^ SBox[roundKey[1][12]];
for (int i = 0; i < 12; i++)//word8~11
roundKey[2][i + 4] = roundKey[2][i] ^ roundKey[1][i + 4];
roundKey[3][0] = roundKey[2][0] ^ roundConstant[2] ^ SBox[roundKey[2][13]];
roundKey[3][1] = roundKey[2][1] ^ SBox[roundKey[2][14]];
roundKey[3][2] = roundKey[2][2] ^ SBox[roundKey[2][15]];
roundKey[3][3] = roundKey[2][3] ^ SBox[roundKey[2][12]];
for (int i = 0; i < 12; i++)//word 12~15
roundKey[3][i + 4] = roundKey[3][i] ^ roundKey[2][i + 4];
roundKey[4][0] = roundKey[3][0] ^ roundConstant[3] ^ SBox[roundKey[3][13]];
roundKey[4][1] = roundKey[3][1] ^ SBox[roundKey[3][14]];
roundKey[4][2] = roundKey[3][2] ^ SBox[roundKey[3][15]];
roundKey[4][3] = roundKey[3][3] ^ SBox[roundKey[3][12]];
for (int i = 0; i < 12; i++)//word 16~19
roundKey[4][i + 4] = roundKey[4][i] ^ roundKey[3][i + 4];
roundKey[5][0] = roundKey[4][0] ^ roundConstant[4] ^ SBox[roundKey[4][13]];
roundKey[5][1] = roundKey[4][1] ^ SBox[roundKey[4][14]];
roundKey[5][2] = roundKey[4][2] ^ SBox[roundKey[4][15]];
roundKey[5][3] = roundKey[4][3] ^ SBox[roundKey[4][12]];
for (int i = 0; i < 12; i++)//word 20~23
roundKey[5][i + 4] = roundKey[5][i] ^ roundKey[4][i + 4];
roundKey[6][0] = roundKey[5][0] ^ roundConstant[5] ^ SBox[roundKey[5][13]];
roundKey[6][1] = roundKey[5][1] ^ SBox[roundKey[5][14]];
roundKey[6][2] = roundKey[5][2] ^ SBox[roundKey[5][15]];
roundKey[6][3] = roundKey[5][3] ^ SBox[roundKey[5][12]];
for (int i = 0; i < 12; i++)//word 24~27
roundKey[6][i + 4] = roundKey[6][i] ^ roundKey[5][i + 4];
roundKey[7][0] = roundKey[6][0] ^ roundConstant[6] ^ SBox[roundKey[6][13]];
roundKey[7][1] = roundKey[6][1] ^ SBox[roundKey[6][14]];
roundKey[7][2] = roundKey[6][2] ^ SBox[roundKey[6][15]];
roundKey[7][3] = roundKey[6][3] ^ SBox[roundKey[6][12]];
for (int i = 0; i < 12; i++)//word 28~31
roundKey[7][i + 4] = roundKey[7][i] ^ roundKey[6][i + 4];
roundKey[8][0] = roundKey[7][0] ^ roundConstant[7] ^ SBox[roundKey[7][13]];
roundKey[8][1] = roundKey[7][1] ^ SBox[roundKey[7][14]];
roundKey[8][2] = roundKey[7][2] ^ SBox[roundKey[7][15]];
roundKey[8][3] = roundKey[7][3] ^ SBox[roundKey[7][12]];
for (int i = 0; i < 12; i++)//word 32~35
roundKey[8][i + 4] = roundKey[8][i] ^ roundKey[7][i + 4];
roundKey[9][0] = roundKey[8][0] ^ roundConstant[8] ^ SBox[roundKey[8][13]];
roundKey[9][1] = roundKey[8][1] ^ SBox[roundKey[8][14]];
roundKey[9][2] = roundKey[8][2] ^ SBox[roundKey[8][15]];
roundKey[9][3] = roundKey[8][3] ^ SBox[roundKey[8][12]];
for (int i = 0; i < 12; i++)//word 36~39
roundKey[9][i + 4] = roundKey[9][i] ^ roundKey[8][i + 4];
roundKey[10][0] = roundKey[9][0] ^ roundConstant[9] ^ SBox[roundKey[9][13]];
roundKey[10][1] = roundKey[9][1] ^ SBox[roundKey[9][14]];
roundKey[10][2] = roundKey[9][2] ^ SBox[roundKey[9][15]];
roundKey[10][3] = roundKey[9][3] ^ SBox[roundKey[9][12]];
for (int i = 0; i < 12; i++)//word 40~43
roundKey[10][i + 4] = roundKey[10][i] ^ roundKey[9][i + 4];
}이제 위 코드들을 AES 구성에 맞게 맞춰주면 AES-128을 얻을 수 있습니다. 그런데 꼭 여러분의 손으로 코드를 짜보셨으면 좋겠습니다. 여기 있는 코드들은 절대 안전한 코드가 아니니 실전에서 사용하지 말아 주세요.
질문은 댓글 남겨주세요.